The people – the physicists – we have encountered here all used experimental
procedures and activities to arrive at their conclusions (often wrong, of
course). They took notes of their findings, pondered the reasons why they were
observing actions and reactions, and then published and discussed their
observations and conjectures. We’ve already seen how clever some were. For
instance, the torsional balance used by Coulomb was extraordinary. To have been
able to measure, not absolutely but relatively, the tiny differences he noted in
the charges placed on materials that he then carefully moved about to determine
the inverse square of the distance relationship of charge repulsion was
extraordinarily beautiful work.

As use of Volta’s battery or versions of the pile became more popular, it was
possible to replicate and then extend the work of others because their results
and findings were repeatable so that knowledge could be verified and then
extended. The investigators noticed that their circuits and apparatus,
interconnected by various materials and mechanisms, often developed heat within
the assemblies. The German physicist Georg Ohm, in 1827 published his
observational findings concerning voltage, current, and lengths of wire. His
findings reported that readings from a galvanometer (a device which measures
current and invented by Hans Oersted in 1820) were directly proportional to the
length, diameter, and type of wire and the voltage applied to the circuit. Today
we know that relationship as I = E / R, R = V / I, and E = I x R[1]. This
equation, known as Ohm’s law, was agreed upon in 1861. It is extremely important
and needs to be committed to memory.

When I was a kid, I asked a fellow how I should go about learning electronics.
He said simply, “all you need to know about electronics is Ohm’s Law”.
Interestingly, he was right. It was not at all obvious, then, how that could be.
Ohm’s Law is so simple – just three terms. I was bored with it in five minutes.
Little did I know then!

The variation in voltage and current due to the length, type, and diameter of
wire came to be called the resistance to the flow of electronic charge. The
definition was set as a proportional relationship between voltage and current
and measured in units to be known as ohms. One ohm is defined to be the
resistance in a circuit passing one amp of current with a potential difference
of one volt. The value ohm is used so often in electronics that it has it’s own special symbol, the Greek letter omega, Ω The majority of electronics is devoted to this simple and
inseparable relationship. The manipulation, measurement, and response to these
three values: current, voltage, and resistance.

Resistance became quite useful for regulating the amount of voltage and current
in a circuit. Soon, devices termed resistors, made from various lengths and
diameters of wire became available to experimenters. Lengths of wire made from
different metals offered a wide variety of resistance values in many different
physical forms. It was discovered (and patented in 1905), that wire made from a
combination of iron, nickel, and chromium (to be called nichrome), offered both
very high resistance and very high heat tolerance. Nichrome wire became very
common for use in all types of heaters, most commonly, toasters. Carbon powder,
compressed into small cylinders, sorted into like values and labeled by their
value, became widely commercially available as devices known as resistors. There
are now a huge variety of resistors made from sputtered metal films, carbon
films, wire, ceramic, and conductive plastics. All have various characteristics
which are useful in all kinds of circumstances. Some resistors vary their value
of resistance based on other physical characteristics such as heat and light.
Heat dependent resistors are useful for varying the amount of current and
voltage in a circuit (which can be measure with a meter) based upon the
temperature that the resistor is being subjected to – a thermistor. Photocells
are light dependent resistors useful for measuring either the amount of light
present, or just the presence or absence of light. When used to detect the
presence of light, a photocell can be used to trigger door openers, turn on
lights when it becomes dark, or count items interrupting a beam to make sure the
right number of candy bars fill a box. Various forms of resistors are all around
us performing useful functions.

The relationship between voltage (E), current (I), and resistance (R) can be
represented by the simple figure below.

E, the symbol for voltage is placed over the I, symbol for current and R, symbol
for resistance. You can remember then that to find the voltage value E, you can
cover it with your finger which will then leave the I and R side by side,
meaning to multiply them together – you need to multiply current by resistance.
In a similar manner, to find out the current, cover the I with your finger
leaving the E to be divided by R. To find the resistance when given the voltage
and current, cover the R and see that you need to divide the voltage E, by the
current I. Hopefully, you can remember this representation of the three values
and their orientation, then be able to recall how to find the needed value given
the other the other two.

[1] E = voltage, I = current, R = resistance

73…W3SEH

Power is how electricity performs work. Whether it’s used to heat a room, run a
motor, or operate a television set, it’s the power that counts. Voltage is the
EMF (electromotive force) that pushes electric current through resistances.
Voltage may be thought of as pressure. Current is amount of electrons that will
perform the work. To quantify power, we use the term Watt, named after James
Watt, the inventor who improved upon the Newcomb steam engine in 1776, which
started the Industrial Revolution.

Power expressed as watts, is computed by multiplying voltage times current,
P=EI. Based upon Ohms Law, there are many other ways to determine power such as
P=I²R, P=E²/R. Many algebraic combinations of P, E, I, and R will be used in
electronics. Memorizing these basic versions now will save you time in the
future.

73… W3SEH

The next property of electricity we need to explore is called voltage. A volt is
another one of those quantities that has been given a name from someone in
history who contributed a significant finding to the field of physics. In this
case, Alessandro Volta from northern Italy who in 1775, may have developed the
first practical battery. At least, he was the first to publish his findings
after he constructed it while it is believed that possibly the Phoenicians or
Greeks may have discovered the properties of a battery much earlier in history.
Since they didn’t publish their findings, they didn’t get the credit. The first
electrical device Volta adapted and publicized in 1775 was quite simple. Two
circular metal plates perhaps six to eight inches in diameter and a quarter inch
thick were assembled. The top plate was fitted with a wooden handle and the
lower plate was coated with wax or pitch. The wax acted as an insulator. The top
plate was briskly rubbed with fur to create a static electric field on the plate
which could then be transferred to other devices by holding the plate with the
insulated wooden handle and touching the plate to something. Placed on the wax
covered plate, the charge would migrate into two parts, a negative charge on the
top of the plate and a positive charge on the bottom of the plate. Both would
remain for long periods of time until discharged by touching to ground and
bleeding off the held charge. Volta called the device an electrophorus but
today, we know it as a capacitor, not really a battery but more a charge storage
device. We’ll talk more about capacitors, a basic electronic device, a bit
later.

The battery came about in 1800 while Volta was disagreeing with his contemporary
colleague, Luigi Galvani, a doctor and anatomy instructor. Galvani had reported
that he was able to cause a dead frog’s dissected legs to twitch by touching the
exposed sciatic nerve with a metal scalpel. Galvani suggested that the frog
muscles were activated by an electrical fluid carried by the nerves. Volta
asserted that the electrical stimulus was created externally to the frog. To
disprove Galvani’s animal electricity theory, Volta assembled plates of
dissimilar metals, silver and zinc, stacking them with separators soaked in salt
water (which he said worked better than plain water) and connecting them to the
frog’s nerve, he could make the legs twitch as well. The ability to create an
electric current without having to rub an object with animal fur was a
significant contribution and was termed the voltaic pile or cell.

Volta’s experiments with his pile revealed some characteristics that had not
previously been known. Increasing the size of the pile also increased the
magnitude of the electric charge it produced. Outside of noting that brine
soaking the separators between the plates produced more charge than plain water,
he did not experiment with other fluidic solutions, what we now call
electrolytes. He noted that different metals used for the plates produced
different charge values. Other investigators would explore the characteristics
of the voltaic pile in great detail and since it permitted drastically more
consistent investigation of electricity, most physicists used similar variations
of the concept as well.

As an interesting aside, Volta happened to read a paper written by Benjamin
Franklin that described a “flammable air” found hovering over lakes. That air
turned out to be methane, created by rotting vegetation at the bottom of lakes.
Volta isolated the gas in 1778 and collected it in vessels to study it from Lake
Maggiore, a large lake along the border of Italy and Switzerland.

By 1830, Michael Faraday noted that the chemical reaction of a salty or acidic
solution with metallic electrodes was the source of the electric current.
Faraday was able to describe the chemical reaction that caused electrons to
collect, or migrate, or flow from one of the electrodes to the other. It became
noted that if the electrodes were connected with a conductor, the electric
charge would flow from areas of higher charge to areas of lower charge. The
higher charged electrode was labeled as negative, the lower charged electrode
was labeled as positive. It was also noticed that the flow of charge did not
necessarily have to be from negative to positive, it just had to be from an area
of more intense charge to an area of less intense charge, or from a more
negatively charged point to a less negatively charged point or from a less
positive area to a more positive area.

Now that we know that electric charges can migrate or move from one point to
another via a conductor (there are many such as copper, silver, gold, aluminum,
and ionic fluids like brine). If we cause one ampere of charge to move through
that conductor in one second, we can say there is a charge potential difference
between the points connected by the conductor of one volt. Voltage then is the
cost in energy required to move a unit of charge. Or, stated differently, it is
the potential difference that will transfer one joule of energy per coulomb of
charge. Wait. Joule? Didn’t we see that in the description of current and the
amount of energy contained within the proton?

Indeed. The joule is a name given to the amount of work done by applying a force
of one newton through a distance of one meter. Or, passing one ampere of
electric current through a resistance of one ohm for one second, or an electric
charge of one coulomb through a potential difference of one volt, and finally
the work of one watt for one second. All these values of energy are equivalent,
just expressed differently using different units.

Voltage is a bit more difficult to explain than the basic electron charge and
the flow of charges, current. Voltage may be thought of as the pressure behind
the charge, pushing it harder and harder as the voltage increases. If there is
no pressure difference between two points, there is no current flow and there is
no voltage. Sometimes it will be necessary to measure a voltage at a point,
which may be a bit confusing to you right now because we just said there had to
be two points. Indeed, it is often assumed that the “second point” which has not
been identified, is a ground potential point. Ground is a neutral reference
point in electronics which permits voltages to be either positive or negative
with respect to that neutral ground.

The abbreviation “V” is used to refer to volts, and usually E or e in equations.
Also, mV for millivolt (1 thousandth of a volt) or uV for microvolt (1 millionth
of a volt).

Now that we have been introduced to the two most common characteristics of
electricity, current and voltage, we can introduce a third, resistance.

73… W3SEH

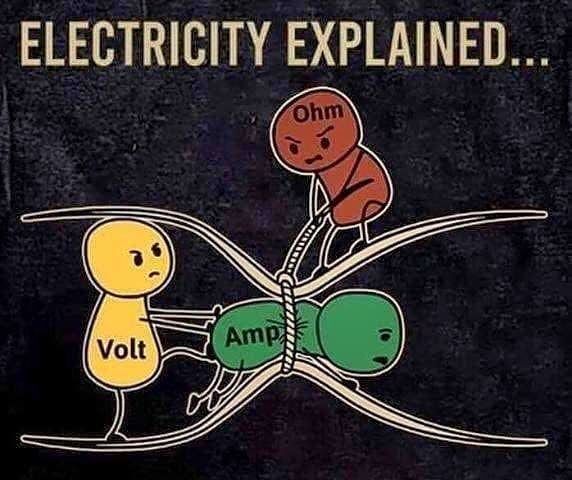
Electrons are now presumed to be a self contained atomic particle, not composed
of anything any smaller, and have a mass of 1/1836 of that of the proton. If you
could get 1836 of those guys glued together, the group would balance a proton on
the other end of a teeny tiny teeter totter. But you couldn’t do that because an
electron is something called a fermion which means only one can occupy a given
space at a time due to a rule called the Pauli exclusion principle and since
they all have a negative charge, they each push the others away from themselves.
The other 1835 guys would have to float around somewhere else, all of them
staying out of the way of each other. At the moment however, we don’t know of
any element that has that many electrons floating around the nucleus anyway so
the 1/1836 value is really only of academic interest. The electron has a charge
of -1.602 x 10^-19 coulomb. Notice that the charge of the electron is negative.
Meanwhile, the charge of the much more massive proton, is +1.602 x 10^-19
coulomb. So, charge-wise, the electron and proton are equivalent but have
opposite signs. When you smoosh one of each together, you get an annihilation of
both particles, a net charge of zero, and the release of gamma rays and photons.
Congratulations, you’ve just learned your first bit about quantum
electrodynamics. Not too bad was it?

Electrons are very mobile, light, and energetic particles. Protons on the other
hand are pretty heavy, comparatively, less energetic, and tend to stay put.
Since the number of protons in the nucleus of an atom of an element determine
the type of element, you don’t want protons moving around and being exchanged
between adjacent atoms. Otherwise, you would have one element changing into
another element unpredictably. You don’t want a dish of carbon changing into
part sulfur and part nitrogen at the drop of a hat. You want that elemental
carbon to stay as it is until purposely caused to change. On the other hand,
since the highly mobile electrons are easily attracted to other protons, those
electrons can be pretty easily shared with the protons in the nucleus of nearby
other elements. This behavior permits elements to combine into molecules of
compound chemicals by sharing electrons yet keeping the protons in the
compound’s elements intact.

The chemistry of elements and compounds comes into play in electronics all the
time. By changing the characteristics of chemicals involved in materials, we can
cause LEDs to emit different colors of light, cause transistors to have
different gain and loss characteristics, and cause different types of
transistors in integrated circuits to operate at different voltages and speeds
of transmission. Chemistry plays vital roles in all areas of electronics,
setting the characteristics of conducting and insulating materials as well.

Back to seeing what those electrons are capable of. Always remember that
electrons are negatively charged. When they move, they move from an area of a
concentrated negative charge to an area of positive (or less negative) charge.
This is really important to understand and remember. Life’s experiences sort of
direct you in the wrong way here, making you think that electricity flows from
the “+” (plus, or red) terminal to the “-” (minus or black) terminal. But no!
That’s not what happens. Its the other way around! When those mobile electrons
move, it causes a current to flow. Just like water flowing in a stream, the
electrons move from a point of higher negative charge to a point of lower
negative charge (or more positive) causing a stream of electron current.
Current flow is the result. From the minus terminal (usually labeled as black-
but not always) to the plus terminal (usually labeled as red, but again, not
always; you always have to be careful about this color labeling business).

Remember that the electric charge of a single electron is -1.602 x 10^-19
coulomb. If we have 1×10¹⁹ electrons flowing from point A to point B, we will
have a charge difference of -1.602 coulomb between A and B. Similarly, if we
happened to have 6.2422 x 10¹⁸ electrons laying around and we got them all to
zoom past an arbitrary point in one second, we’d have exactly 1 ampere of
current flowing past that point. (6.2422 x 10¹⁸ x |-1.60210^-19| = 1.0). If,
however, we had only 3.1211 x 10¹⁸ electrons, and it still took them that one
second to pass that arbitrary point, we’d only have half an ampere of current
flow. The charge of each electron remains constant but we have only half as many
electrons as before so the quantity of current flow is half as much. Current
flow then, measured and expressed in amperes, is defined as 1 coulomb of charge
flowing past a point in 1 second. To have current, you have to have movement of
the electrons and their associated charge.

That’s pretty simple. So, what’s a coulomb? The short answer is that it is the
arbitrary name given to a measure of the combined amount of electric charge on
6.2422 x 10¹⁸ electrons. The long answer is a bit more involved and puts us down
a rabbit hole that leads to a whole different world of stuff called atomic and
quantum theory. This is actually pretty cool stuff and all links together pretty
nicely but leads us into looking at some pretty scary mathematics.

6.2422 x 10¹⁸ electrons sounds like quite a few electrons. Is there some way to
get a feeling for how much that really is? Sure, let’s use an amount of iron to
see how big of a pile of it we would have to have to accumulate that many
electrons. Since iron has an atomic number or weight of 26, that means that a
single atom of iron has 26 protons in its nucleus. Since there are 26 protons,
there are also 26 electrons. If we divide 6.2422 x 10¹⁸ by 26 we have 2.4008 x
10¹⁷, still a pretty big number. Since electrons don’t have any mass, it is the
mass of the protons that is going to account for the mass in this accumulation
of iron. The mass of a proton is about 938 MeV/c². Oops, that looks like it
isn’t going to be as straight forward as it was looking, I was hoping for grams.
But no. MeV by the way is million electron volts and c² is the speed of light
squared.

938 million electron volts divided by the speed of light squared. Volts and the
speed of light? Well, we’ll get to volts in a little while so maybe we stumbled
across something useful. But the speed of light? What’s that got to do with it?
Well, you’ve probably heard of Albert Einstein and his famous equation E = mc2.
That equation established that mass and energy are directly proportional to each
other and related by the speed of light squared. What that means is, a given
mass of matter has a lot of energy in it, that mass and energy are equivalent,
and that mass and energy can be converted to each other. Those electron volts
are really a measure of the amount of energy contained within the proton
expressed in joules.

As we’ve just seen, its hard to talk about things in physics, electronics, and
chemistry without encountering that equal sign in Einstein’s equation. Mass and
energy are equivalent, we can’t have one without the other. The equivalence is
so common that it has been simplified to the value of 1 GeV/c² = 1.783 x 10^-27
kg. A really small mass of 1.783 x 10^-27 kilograms is equivalent to 1 giga
electron volts accelerated to the speed of light squared.

Our proton mass then equates to 0.938 x 1.783 x 10^-27 kg, 938 MeV/c² divided by
1 GeV/c² or 1.6725 x 10^-27 kg per proton. Multiply that by 2.4008 x 10¹⁷
protons and our pile of iron should have a mass of 4.0153 x 10^-10 grams. A
really small amount! A coulomb of electrons is contained within that tiny amount
of iron.

Lets stop for a minute and explain some things.

This coulomb stuff is just an arbitrary name given to the measure of electric
charge. We’ll get back to that in a minute. First, note that we are going to run
into all kinds of things that have these arbitrary names. Names like Ohms, Volt,
Ampere, Henry, Farads. All these names have quantities of “stuff” associated
with them. The “stuff” is all different, which is why they have different names
and they are not equivalent. Although, in some cases, one type of quantity of
stuff may be expressed as some other quantity of other stuff, both related by
some numeric quantity. We’ll try to point those cases out when we run into them.
For now, note that each of these names refer to some person who, back in
history, discovered and then described the physical characteristics of a
particular property of material, a process, or an effect. Their name has then
been ascribed to each of these properties in order to be able to conveniently
refer to them. Each of these historical people have extremely interesting
stories associated with them. How they first noticed the property of matter that
became associated with their name, how they developed techniques to quantify or
measure the property, and subsequently, how their discovery led to our further
understanding of the nature of the characteristics of the universe. There are
lots of these names and it will become important to understand each of the
properties of matter that the name refers to so that eventually, you have a
complete understanding of the full nature of the sciences associated with
electronics. Although there are lots if these names, they will become familiar
and their meaning will eventually be comfortable to you. I urge you to explore
the stories of each of the people whose names we will be using. Almost every one
of the stories is interesting and the remarkable thing is just how long ago
their discoveries were made. Think of how observant, then curious and clever
they were to have worked out their contributions to knowledge of the universe.
The question is, will you be as clever and make such an important a contribution
as any of them? Note that as time passed, nearly each of those people studied
the discoveries of their predecessors, came to understand the previous
discoveries, then used that previous information to formulate their own
contributions. Nobody understood it all to begin with. Interestingly, just think
about all the information that is available to you, right now, that those folks
did not have available to them in their lifetimes!

Ok, let’s get back to the coulomb. Wait a minute, who says the electric charge
of an electron is -1.602 x 10^-19 coulomb? How did they figure that out? Actually
Robert Milliken figured it out in 1909 by performing his famous oil drop
experiment. The reason its famous is because it finally determined what the
electric charge on a single electron was. How? By determining how many electrons
were in a tiny drop of oil which he was able to suspend in mid-air by applying
opposite electrostatic potentials to two plates which allowed the oil drop to
float in mid-air. By carefully measuring the electrostatic potential, and
knowing roughly how many molecules of oil were in the drop and thus how many
protons and electrons, it was possible to calculate the amount of charge that
had to be applied to all of the electrons to get the molecules of oil to
overcome the attraction of the force of gravity. Dividing the amount of charge
by the number of electrons results in the charge contributed by a single
electron.

How many molecules of oil were in the drop? Well, if we make a whole bunch of
drops, count how many of the drops it takes to comprise a given volume, say ten
cubic centimeters, then divide 10 cc by that number of drops, we can pretty
closely determine the volume of a drop. Since they could determine the density
of the oil, the mass of a droplet could be determined. The mass then reveals the
number of molecules. Knowing the number of molecules and the chemical formula of
the oil tells us how many atoms of each element make up the molecules and then
how many protons and electrons are contained in that volume of oil within the
droplet. Very clever progressive reasoning. Won him a Nobel prize.

It gets a bit more complicated and involved to fully explain a coulomb because
it also involves forces in different directions or vectors, so let’s try to
simplify it a bit and leave the full explanation for you to discover some other
time. In about 1777, a French physicist named Charles Coulomb developed a device
called a torsional balance which is a very sensitive mechanism for measuring the
amount of force applied to a fine fiber, spring, or wire. By using the torsional
balance, Coulomb determined that electrically charged materials – probably
copper or brass spheres (with a static charge applied by rubbing those materials
with probably cat fur) repelled each other with forces that varied directly
(which means that the effect is mathematically described within the numerator of
an equation) by both the amount of charge that was on the material (determined
probably by the number of times he rubbed the material with the fur), as well as
inversely (the effect is is described in the denominator of an equation) by how
far apart two pieces of the materials were. In fact, the repellant forces
decreased by 1/4 when the distance doubled and by 1/16 when the distance
quadrupled. So, in 1785 he was able to say that the repellant forces varied
inversely as the square of the distance between them. That’s about all that
could be determined back then. It remained a while (actually 1861 when published
by James Maxwell) before it was noted that the electric charge (the value in the
numerator) influenced things at the speed of light (determined by a number of
investigators moderately accurately between 1676 and 1862) and how well the
materials involved could become magnetic (called magnetic permeability and
described by mathematics developed by Oliver Heaviside in 1885). Together then,
Coulomb’s initial observations were refined by many famous names that appear in
physics until a value for the unit electrical charge on an electron was finally
determined in 1909.

And there we have it. We have learned how physicists figured out the first
property of electricity: current. And what current really is: the quantity of
unit electric charges flowing past a point in a given amount of time. One ampere
or amp of current consists of 6.2422 10¹⁸ electron’s worth of unit charges
flowing past a point in one second. The ampere was named for Andre-Marie
Ampere, a French professor of physics and chemistry born a year before America
declared its independence. Ampere demonstrated the relationship between current
flow and magnetics by showing that two parallel wires attracted or repelled each
other proportionally depending upon the length of the wire and the current they
carried. The ampere is abbreviated “A” or called amp and is usually referred to
as “I” in equations. Other values may be expressed as milliamperes, milliamps,
or ma (1 thousandth of an ampere), or microamp (1 millionth of an amp). Next
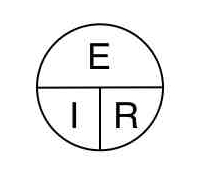
we’ll explore the volt and then we will have learned about two of the three
elements of the most basic equation of electronics, ohms law. From there,
everything else is down hill.

73… W3SEH

I didn’t learn about electronics correctly. It wasn’t taught to me in an orderly
fashion. High school and junior high school teachers didn’t begin one day and
say, “OK, today we’ll learn all about electronics in a couple of hours”. Nope,
it was not accomplished in that manner at all. I had no idea that all this other
stuff we were taught in science classes would eventually come together to reveal
the workings of electronics. Perhaps if my teachers had said that all this was
going to be about electronics at the time, I would have been more interested and
paid more attention. It was fed to us over a period of months and years a
teaspoonful at a time with no cohesive direction or meaning by lots of different
teachers. Its nuances, derivations, historical contexts, and associations were
not presented in opportune circumstances. Consequently, the elegance of the
field escaped me for the longest time and I was denied an overall appreciation
of the interlocking disciplines of physics, chemistry, thermodynamics, and
mathematics. Thermodynamics? Say what? Relax, merely a medium sized word
meaning the movement of heat, like air conditioning in August. There is no
possible way I could now assert that I am expert, or even sufficiently
conversant in the subject to warrant that I will be successful in teaching you
an appreciation of electronics. What I would like to try though is to convey to
you some of those realizations and revelations that have intrigued me and led me
to maintain a continued interest in the subject. In doing this, perhaps I can
pique your interest sufficiently for you to be inspired enough to continue
exploration and discovery on your own from other sources.

This blog is a VERY short introduction to electronics, a subject than can entail
many, many feet of bookshelf space to cover a reasonable understanding of the
subject. Electronics is such a broad field, contains many sub-areas of
expertise, that is will seem daunting to you at first, even discouraging to
think of undertaking it. From components, to circuits, to devices, and entire
fields of study, electronics can be a lifelong interest or a lifelong career.
Hopefully this blog can get you started in a short time so that you can explore
all the other possible paths at your own convenience.

This blog draws heavily upon a few reference texts that have proven useful to me
over the years. The first is Electronic Communication by Robert L. Schrader. I
have a couple editions of this book but I don’t know if it is still in print. If
not, it should be readily available from used book stores, it has been an
excellent and very widely used text for many years. I have used Shrader’s book to a wide degree is this blog because of the clarity of presentation, thorough explanation at this level of understanding, and brevity of complexity. This blog conveys an introduction, not a PhD thesis on the subjects. Additionally, I also usedthe Art of Electronics by Paul Horowitz and Winfield Hill. This book is still in print and is a very comprehensive (an understatement) text on the basics of components and circuit design. Wading into the Art of Electronics, it would be
advised to start with a book like Schrader’s first.

To fully and truly understand the field, you are going to have involve yourself
in mathematics. There is no escaping it because all the disciplines of physics
interact – they are all related and impact and influence each other. The only
way to appreciate that is with the use of mathematics. Optics, magnetics,
electrodynamics (the physics of the movement of atoms and their constituents)
and more are all involved. Albert Einstein tried his best to derive a set of
equations and mathematics that completely encompass all the electric, magnetic,
and atomic forces. He was not successful within his lifetime, nor has anyone
else yet accomplished what is called a “unification” theory. Consequently, and
just perhaps, there may not be a unification. It may remain a collection of bits
and pieces of understanding and conjecture and observation that defy a single,
overall cohesive description. By earth humans at least. Proficiency in algebra
and trigonometry are required to obtain skills and comfort in basic electronics.
To fully understand what happens when electronics are involved in motion or
radio or optics will require knowledge of calculus because stuff moves. Calculus
is mathematics that describes the behavior of things when they change position
or value over time, in other words, are dynamic. Doesn’t take too much to get
things moving in electronics. Calculus comes to the rescue to explain why things
happen.

We can begin with a description of what the field of electronics is. It is a
very broad area comprising many individual elements and combinations of those
elements in lots of different ways. For example, light, electricity, chemistry,
and physics all combine to yield the intriguing device, a Light Emitting Diode
or LED. Seems a pretty simple device – but not. First developed in the early
1970’s, only recently have blue and white ones become available. Now draped over
Christmas trees in many different colors, originally it was possible to
fabricate LEDs that radiated only red light. Even then, the fact that the light
was available without the high temperatures associated with the glowing
filaments of incandescent bulbs caused many of us to delight in holding a
glowing LED in our fingers, marveling in the light available without heat.
Nothing short of magic. Same with WiFi. Instantaneous high speed data
communications between you and someone halfway around the world via the internet
without an intervening wire or even wet string. Again, nothing short of magic.
Silent, high speed motors that rotate the platters inside hard disk drives and
DVD players. Again, elements of the field of electronics. Television, LCD
display screens, MRI (magnetic resonance imagery), the 3D movie Finding Nemo,
and the recorded music sung by Mariah Carey. Once again, all made possible by
elements of electronics. GPS navigation, cell phones, fish finders, weather
radar, cash registers, microwave ovens, air conditioning thermostats, probably
your wrist watch. Yep, all composed of combinations of elements of electronics.
Aren’t you curious about how all those things work? Surprisingly, as different
as they all are, they are also remarkably similar. The field of electronics then
merely simplifies to the activity of manipulation and movement of electrons to
perform useful functions and work.

73… W3SEH